Наиболее значимые результаты исследований лаборатории теоретической физики

Краевые состояния экситонного диэлектрика при наличии
спин-орбитального взаимодействия

Автор: В.В. Вальков

 

Известно, что спин-орбитальное взаимодействие и инвертированный характер электронной структуры имеют существенное значение для реализации топологического изолятора. Для него топологический индекс энергетической структуры имеет нетривиальное значение, а в геометрии открытых границ возникают краевые состояния.

Инвертированность зонной структуры является существенной и для формирования экситонного диэлектрика (ЭД). Поэтому представляется актуальным изучение условий, при которых в ЭД при открытой геометрии могут возникать краевые состояния.

В работе на примере энергетической структуры квантовой ямы HgTe рассмотрены допустимые фазы ЭД, различающиеся симметрией экситонного параметра порядка (ЭПП) и значениями топологического индекса.   

Показано, что без учета обменного взаимодействия существуют три фазы ЭД с s–, d– и p– типами симметрии ЭПП. В p–фазе значение топологического инварианта соответствует нетривиальной топологии, и в геометрии открытых границ имеются решения, соответствующие краевым состояниям. Однако эта фаза является метастабильной. Стабильной является s– фаза с тривиальной топологией.

Ситуация существенно изменяется при включении обменной части кулоновского взаимодействия. В этом случае основным состоянием ЭД становится фаза с s+d– симметрией ЭПП. Главная особенность s+d– фазы заключается в том, что для нее топологический инвариант имеет нулевое значение, но, несмотря на это, в геометрии открытых границ реализуются краевые состояния (см. рисунок).

 

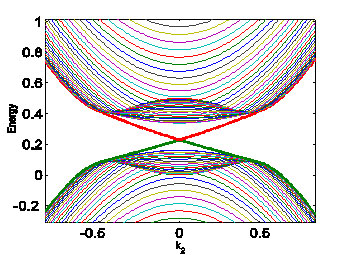
Энергетический спектр фермионных состояний s+d – фазы ЭД при учете спин-орбитального взаимодействия в геометрии открытых границ. Фермиевские состояния, соответствующие двум ветвям спектра, расположенным в запрещенной зоне (зеленая и красная линии) со значениями квазиимпульса, находящимися в окрестности центра зоны Бриллюэна, являются краевыми.  

 Вальков В.В.
Краевые состояния экситонного диэлектрика со спин-орбитальным взаимодействием //
Письма в ЖЭТФ. – 2020 – том 111 – вып. 11 – с. 772-777. (Impact Factor WoS – 1.399, Q3)

 

Новый диаграммный подход к проблеме сильного взаимодействия фермионов с подсистемой квантовой спиновой жидкости в купратах

Авторы: В.В. Вальков, В.А. Мицкан, М.М. Коровушкин, Д.М. Дзебисашвили

В рамках спин-фермионной модели электронного строения купратных сверхпроводников разработана диаграммная форма теории возмущений, позволившая корректно описывать сильную связь подсистемы спинов ионов меди, находящейся в состоянии квантовой спиновой жидкости, с кислородными дырками. Массовый оператор спин-фермионной связи представляется в виде перестроенного ряда, слагаемые которого содержат бесконечные последовательности диаграмм с одноцентровыми, двухцентровыми и т.д. корреляторами. Суммирование всех графиков с одноцентровыми корреляторами позволило точно учесть главный вклад сильной спин-фермионной связи, определить большую величину энергии связи спин-поляронных квазичастиц и воспроизвести важные особенности спектра фермиевских возбуждений. В частности, ренормировки приводят к формированию локального минимума фермиевского спектра в окрестности точки (π/2, π/2) зоны Бриллюэна. Учет вкладов в массовый оператор, определяемых двухцентровыми корреляторами, приводит к спектральным свойствам, хорошо согласующимся с экспериментальными данными по купратам.

 

 

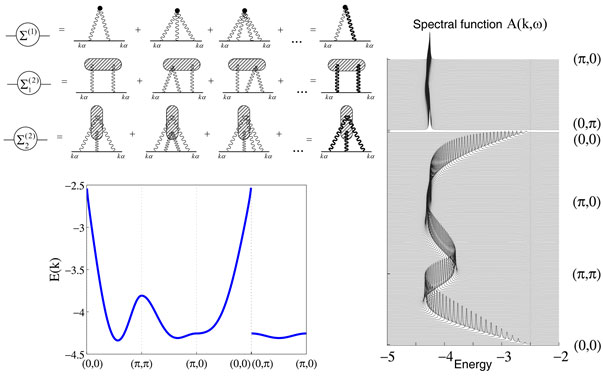
Диаграммы для массового оператора (слева вверху), энергетический спектр (слева внизу) и спектральная интенсивность (справа) φ-d-модели.

 Val’kov V. V., Mitskan V. A., Korovushkin M. M., Dzebisashvili D. M., Barabanov A. F.,
Diagram approach to the problem of the normal phase properties of the spin-polaron ensemble in cuprate superconductors //
J. Low Temp. Phys. 2019.V.197. P.34.

 

  Каскад квантовых переходов и магнетокалорические аномалиив открытой нанопроволоке

 Авторы: Вальков В.В., Мицкан В.А., Шустин М.С.

  Предсказано аномальное поведение магнетокалорического эффекта в нанопроволоке конечного размера со спин-орбитальным взаимодействием Рашбы и наведенным потенциалом сверхпроводящего спаривания при изменении магнитного поля h. Природа аномалий связана с каскадом квантовых переходов, реализующихся в нанопроволоке в результате смены фермионной четности её основного состояния при изменении h. Обнаруженные особенности, магнетокалорического эффекта сохраняются при учете кулоновских взаимодействий.

 

Зависимость магнетокалорического эффекта от магнитного поля для цепочки из 30 узлов при температуре , наведенном потенциале сверхпроводящего спаривания  и спин-орбитальном взаимодействии Рашбы . Штриховые лини соответствуют поведению магнетокалорического эффекта в замкнутой цепочке с периодическими граничными условиями, сплошные – в разомкнутой.

 В.В. Вальков, В.А. Мицкан, М.С. Шустин
Каскад квантовых переходов и магнетокалорические аномалии в открытой нанопроволоке //
Письма в ЖЭТФ т. - 106, в. 12 (2017).

 

 

1. При учете процессов рассеяния на спиновых флуктуациях развита теория сверхпроводящей фазы с d-типом симметрии параметра порядка, экспериментально наблюдаемая в купратных оксидах. Показано, что при описании спин-флуктуационных процессов рассеяния важную роль играют впервые введенные сотрудниками лаборатории аномальные компоненты силового оператора. Это приводит к модификации уравнений Горькова и существенно сказывается при вычислении аномальных средних в подсистеме фермионов Хаббарда [В.В. Вальков и др. ЖЭТФ 134, 1167 (2008)].
2. Впервые показано, что межузельное кулоновское взаимодействие в Мотт-Хаббардовских диэлектриках приводит к расщеплению нижней хаббардовской зоны на две подзоны [V.V. Val’kov et al. Eur. Phys. J. B 69, 219 (2009); В.В.Вальков и др. ЖЭТФ, 139, 126 (2011)], как только характерная величина этого взаимодействия становится сравнимой, или превышает кинетическую энергию фермионов Хаббарда. Существенно, что спектральная интенсивность нижней зоны (зоны флуктуационных состояний) зависит от среднеквадратичной флуктуации чисел заполнения и растет при повышении уровня легирования.

   

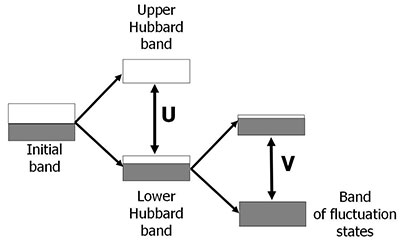
   Схема расщепления энергетических зон сильно коррелированной системы под влиянием
   одноузельного и межузельного кулоновского взаимодействий электронов.

3. В рамках эффективной модели для двумерной решетки Кондо развита теория сверхпроводящей фазы ансамбля спиновых поляронов. При учете эффективных взаимодействий между такими квазичастицами построена фазовая диаграмма, определяющая область реализации сверхпроводящей фазы [В.В. Вальков и др. Письма в ЖЭТФ 88, 426 (2008)].
4. Для реальной структуры CuO₂-плоскости купратных сверхпроводников получена энергетическая структура нелокальных спиновых поляронов и рассмотрена куперовская неустойчивость в ансамбле таких фермиевских квазичастиц.

   

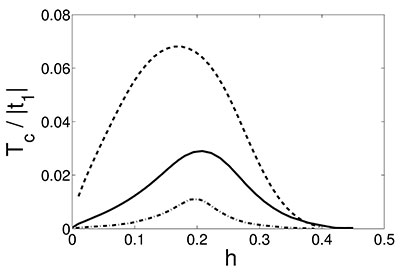
   Концентрационные зависимости T_c при конечных (сплошная кривая) и
   нулевых (пунктир) значениях магнитных корреляторов.

   Нелокальный спиновый полярон формируется из-за обменного взаимодействия спинового момента кислородной дырки со спиновыми моментами двух ближайших ионов меди. Вычисленная на основе диаграммной техники амплитуда рассеяния нелокальных спиновых поляронов в куперовском канале показала сильную взаимосвязь спиновых и зарядовых степеней свободы [В.В. Вальков и др. Письма в ЖЭТФ 92, 683 (2010)].

5. В рамках периодической модели Андерсона в пределе сильных электронных корреляций развита теория сверхпроводящего состояния с s-типом симметрии параметра порядка [В.В.Вальков и др. Письма в ЖЭТФ, 84, 251 (2006); В.В.Вальков и др. ЖЭТФ, 134, 791 (2008)] (переход в такое состояние экспериментально наблюдался в недавно открытом тяжелофермионном скуттерудите LaFe₄P₁₂. Получены точные представления функций Грина сверхпроводящей фазы через нормальные и аномальные компоненты массового и силового операторов. Показано, что при описании сверхпроводящей фазы существенную роль играют аномальные компоненты силового оператора, отражающие спин-флуктуационные процессы в локализованной подсистеме. В однопетлевом приближении эти компоненты вычислены из решения бесконечной системы интегральных уравнений самосогласования для сверхпроводящей фазы. Численные расчеты показали, что включение процессов рассеяния на спиновых флуктуациях приводит к ренормировке критической температуры до экспериментально наблюдаемой.

6. В условиях скоса подрешеток в магнитном поле развита теория антиферромагнитных редкоземельных интерметаллидов с тяжелыми фермионами [V.V.Val’kov et al. Physica B: Condensed matter, 378-380, 692 (2006)]. При учете перестраивания структуры магнитной подсистемы выявлены низкотемпературные особенности электронной теплоемкости тяжелофермионных антиферромагнетиков с металлическим типом основного состояния [В.В.Вальков и др. ТМФ, 162, 125 (2010); В.В.Вальков и др. ЖЭТФ 137, 341 (2010)]. Рассчитанные температурные зависимости намагниченности, теплоемкости и константы Зоммерфельда в окрестности точки перехода в антиферромагнитную фазу качественно хорошо коррелируют с экспериментальными данными, полученными для тяжелофермионных антиферромагнетиков PuGa₃, Ce₂Au₂Cd, YbNiSi₃, PuPd₅Al₂.

7. Совместно с сотрудниками лаборатории сильных магнитных полей предложена модель шоттковских центров в CuO_x цепочках соединения YBa₂Cu₃O_6+x [К.А. Шайхутдинов и др. Письма в ЖЭТФ 92, 369 (2010)], позволившая объяснить экспериментально наблюдаемые особенности изменения низкотемпературной теплоемкости в магнитном поле. Предполагается, что при возрастании концентрации кислорода образуются уединенные ионы меди Cu2+ и пятиионные Cu-O-Cu-O-Cu комплексы, энергетическая структура которых формируется при учете кристаллического поля кубической симметрии с орторомбической добавкой, спин-орбитальным взаимодействием и расщепления в магнитном поле.

8. Для редкоземельного интерметаллида CeRhIn₅ развита теория [В.В. Вальков и др. Письма в ЖЭТФ 95, 390 (2012)], позволившая объяснить сверхпроводящее состояние в окрестности квантовой критической точки, в которой индуцируется дальний антиферромагнитный порядок.

   

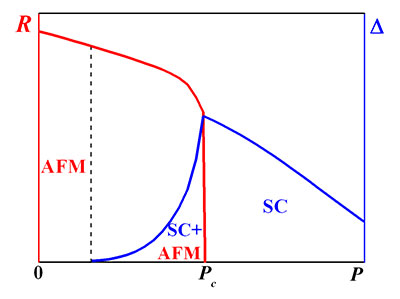
   Зависимости антиферромагнитного R и сверхпроводящего Δ параметров порядка от внешнего давления для редкоземельных интерметаллидов с тяжелыми фермионами. Показаны области реализации антиферромагнитной фазы (AFM), сверхпроводящей фазы (SC) и фазы сосуществования сверхпроводимости и антиферромагнетизма (SC+AFM).

   Показано, что куперовское спаривание и антиферромагнитное упорядочение возникают в результате эффективного обменного взаимодействия, обусловленного процессами гибридизации между p-электронами индия и высокоэнергетическими состояниями подсистемы ионов церия. Определена область давлений, для которой реализуется микроскопически однородная фаза сосуществования сверхпроводимости и антиферромагнетизма.

9. Показано, что при квантовом фазовом переходе с разрушением дальнего антиферромагнитного порядка происходит значительное расширение поверхности Ферми и сильная перенормировка эффективной массы электронов, как это наблюдается в CeRhIn₅. Указанные особенности связаны с перестройкой зоны тяжелых фермионов при переходе через квантовую критическую точку.
10. В рамках спин-фермионной модели показано, что спин-поляронная концепция позволяет воспроизвести тонкие особенности эволюции ферми-поверхности в высокотемпературном сверхпроводнике La_2-xSr_xCuO₄ в нодальном направлении при изменении уровня допирования x [Д.М. Дзебисашвили и др. Письма в ЖЭТФ, 98, 596 (2013)].

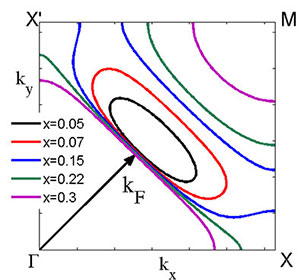
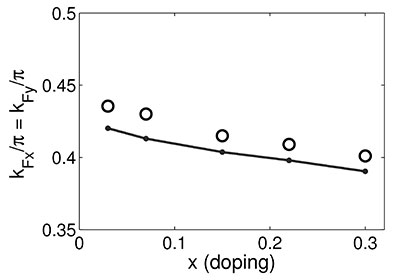
    Поверхности Ферми в первом квадранте зоны Бриллюэна для пяти значений допирования x.	Зависимость импульса Ферми kF от степени легирования x. Сплошная линия - рассчитанные в рамках спин-поляронного подхода, значения kF. Светлыми кружками обозначены, представленные в работе [T. Yoshida et al., J. Phys.: Condens. Matter, 19, 125209 (2007)] экспериментальные значения kF

    Определяющими при этом являются спин-коррелированные перескоки носителей тока и изменение с допированием обратной магнитной корреляционной длины.

11. На основе эффективного гамильтониана 2D модели Эмери в рамках спин-поляронного подхода исследовано влияние спиновых и многоцентровых спин-зарядовых корреляторов на спектральные свойства купратных высокотемпературных сверхпроводников [В.В. Вальков и др. ЖЭТФ, 145, 1087 (2014)]. В результате самосогласованных вычислений установлено, что учет концентрационно-зависимых многоцентровых спин-зарядовых корреляторов, входящих в дисперсионное уравнение, обеспечивает понижение энергии системы и существенно влияет на характер эволюции ферми-поверхности при дырочном допировании.

    

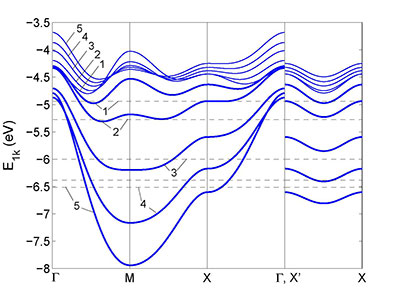
    Дисперсионные кривые нижней зоны спиновых поляронов. Жирные кривые рассчитаны при учете всех корреляционных функций для пяти значений степени легирования: 1) x=0.03; 2) x=0.07; 3) x=0.15; 4) x=0.22; 5) x=0.3. Пунктирной линией обозначено положение химпотенциала. Тонкими линиями показаны дисперсионные кривые, рассчитанные для тех же значений x,
    но при учете только спиновых корреляторов.

12. Показано, что сильная связь между спиновыми моментами ионов меди и кислородных дырок, возникающая в результате процессов гибридизационного смешивания двух дырочных подсистем в исходной модели Эмери, влияет не только на формирование спин-поляронных квазичастиц, но и обеспечивает эффективное притяжение между ними через обменное взаимодействие [V.V. Val'kov et al. Physics Letters A, 379, 421 (2015); V.V. Val'kov et al. Journal of Low Temperature Physics,181, 134 (2015)]. Это индуцирует куперовскую неустойчивость с d-волновым спариванием в 2D-ансамбле спин-поляронных квазичастиц. Полученная в рамках такого подхода фазовая T-x- диаграмма хорошо коррелирует с имеющимися экспериментальными данными.

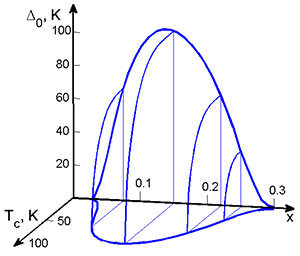
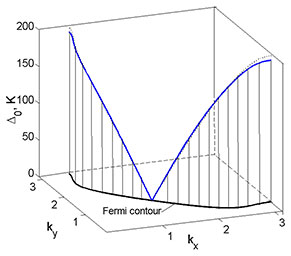
    Изменение амплитуды d-волнового сверхпроводящего параметра порядка Δ0 и температуры перехода в сверхпроводящую фазу Tc при легировании	Зависимость сверхпроводящей щели от квазиимпульса на контуре Ферми. Контур Ферми изображен сплошной линией в горизонтальной плоскости.

13. В рамках модели Шубина-Вонсовского для режима слабой связи на основе механизма Кона - Латтинжера определены области реализации сверхпроводящих фаз с d_xy-, p-, s- и dx²-y²-симметриями параметра порядка. Показано, что для эффективного взаимодействия в куперовском канале существенную роль играют не только одноузельные, но и межузельные кулоновские корреляции. Этот факт продемонстрирован на примере качественного изменения и усложнения фазовой диаграммы сверхпроводящего состояния. Вскрыт механизм индуцирования сверхпроводящей фазы при учёте поляризационных вкладов во втором порядке теории возмущений по кулоновскому взаимодействию. Проведено сравнение полученных результатов по угловой зависимости сверхпроводящей щели в различных каналах с экспериментальными данными по фотоэмиссии с угловым разрешением (ARPES).

    

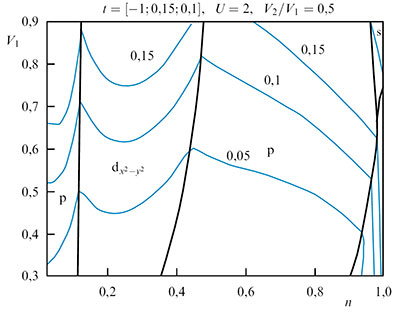
    Фазовая диаграмма сверхпроводящего состояния Кона-Латтинжера в рамках модели Шубина-Вонсовского на квадратной решетке.

    Проанализировано влияние дальних перескоков на фазовую диаграмму и критическую температуру сверхпроводящего перехода в различных каналах. Определены условия возникновения сверхпроводимости Кона-Латтинжера с dx2-y2-типом симметрии и высокими значениями критической температуры Tc~100 K вблизи половинного заполнения.

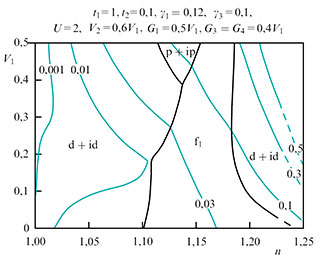
14. В рамках механизма Кона-Латтинжера изучено влияние кулоновского взаимодействия в ансамбле дираковских фермионов на формирование сверхпроводящего спаривания в однослойном и бислойном легированном графене без учета ван дер-ваальсовского потенциала подложки и примесей. Показано, что учет ренормировок Кона-Латтинжера и учет межузельного кулоновского взаимодействия существенно сказываются на конкуренции между сверхпроводящими фазами с f-, p+ip- и d+id-симметриями параметра порядка. Продемонстрировано, что в случае идеализированного бислоя графена с включенным межслойным кулоновским взаимодействием между электронами происходит существенное повышение критической температуры перехода в сверхпроводящую фазу.

    

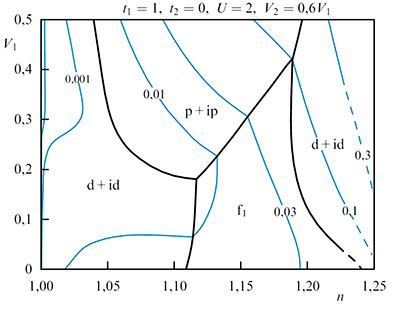
    Фазовая диаграмма сверхпроводящего состояния Кона-Латтинжера идеализированного монослоя легированного графена.

    Кристаллическая структура бислоя графена типа AB.	Фазовая диаграмма сверхпроводящего состояния Кона-Латтинжера идеализированного бислоя легированного графена.

15. Развита микроскопическая теория транспортных свойств магнитных многоуровневых структур атомного масштаба с учетом процессов многократного неупругого рассеяния.
16. Обнаружен эффект отрицательной дифференциальной проводимости, спиновой фильтрации и колоссального магнитосопротивления у магнитных атомных структур.

    

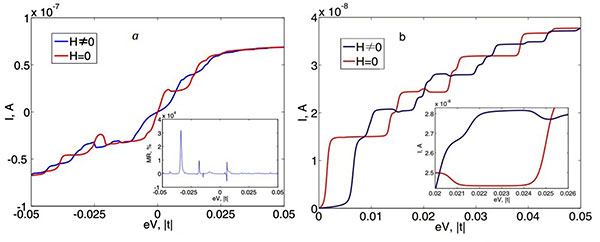
    Влияние магнитного поля (H) на вольт-амперные характеристики анизотропного магнитного атома. Вставка рис. a: колоссальное магнитосопротивление. Вставка рис. b: отрицательная дифференциальная проводимость.

17. Проведено развитие квантовой теории анизотропных гейзенберговских магнетиков с четырьмя магнитными подрешетками.

    В рамках такого подхода вычислен спектр элементарных возбуждений 1D магнетика catena-[Fe^II(ClO₄)₂{Fe^III(bpca)₂}](ClO₄) (далее SCM-catena) с чередующимися, взаимно ортогональными плоскостями легкого намагничивания магнитоактивных ионов железа и показано, что вид спектра возбуждений соединения аналогичен спектру эффективного двухподрешеточного легкоосного магнетика [В.В. Вальков и др. Известия РАН. Серия физическая (2015)].

    Исходя из данных о магнитной структуре и спектральных свойствах указанного соединения, было строго показано, что эффективной низкоэнергетической моделью SCM-catena является обобщенная модель Изинга. Использование этого факта позволило, используя метод трансфер-матрицы, описать экспериментально наблюдаемую аномально сильную модификацию температурной зависимости магнитной восприимчивости соединения при облучении [В.В. Вальков и др. Письма в ЖЭТФ (2014)].

    Также был получен вывод о том, что наличие плоскостей легкого намагничивания в соединении SCM-catena приводит к существенному развитию квантовых флуктуаций, которые должны быть учтены при феноменологическом описании его магнитных свойств в рамках обобщенной модели Изинга. При этом была исследована модификация магнитной структуры соединения при его оптическом облучении [В.В. Вальков и др. ЖЭТФ, (2015)].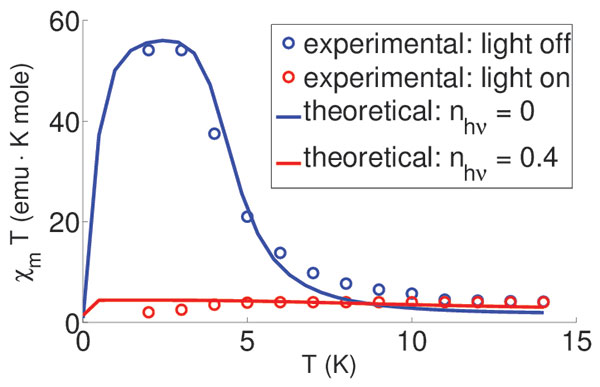

    

    Модификация температурной зависимости магнитной восприимчивости catena-[{Fe^IIClO₄)2FeIII(bpca)₂]ClO₄: а) облучения нет: синяя кривая-теория; синие кружки – эксперимент; б) облучение включено: красная кривая-теория; красные кружки – эксперимент.

18. Определена магнитная фазовая диаграмма и эффективный магнитный момент твердых растворов Yb_xMn_1-xS по концентрации. Для всех составов найден полупроводниковый тип проводимости в Yb_xMn_1-xS. Обнаружены и интерпретированы максимумы в термоэдс в области высоких температур. Обнаружен магнитоемкостный и магниторезистивный эффекты для всех составов Yb_xMn_1-xS с максимальной величиной для х = 0.2 при температурах выше комнатной. Установлена смена знака магнитосопротивления с отрицательного на положительный при нагревании в области составов 0.1 ≤ x ≤ 0.2. Определена критическая температура, выше которой исчезает магнитосопротивление.
19. Обнаружен острый максимум в электросопротивлении в твердых растворах Сe_xMn_1-xS, температура которого смещается в сторону низких температур с ростом концентрации церия. Найдена температура кроссовера от туннельного к активационному типу проводимости. Для двух составов найден интервал температур с электронным типом проводимости, а для состава с х=0.05 обнаружен дырочный тип проводимости. Установлен сдвиг температуры максимума электросопротивления образцов Сe_xMn_1-xS в магнитном поле для двух составов и рост электросопротивления для состава с х=0.05 в магнитном поле. Найден рост магнитосопротивления из вольт-амперных характеристик с увеличением концентрации. Установлена зависимость магнитосопротивления от тока.
20. В твердом растворе Gd_xMn_1-xS для трех составов с Х=0.1, 0.15 и 0.2 найдено магнитосопротивление при температурах в несколько раз превышающих температуру перехода в магнитоупорядоченное состояние. Для всех составов обнаружен полупроводниковй тип проводимости с небольшим минимумом в области высоких температур. Рост сопротивления в магнитном поле связан с уменьшением подвижности носителей тока и обусловлен орбитальным упорядочением электронов с образованием электрической поляризации. Определен максимум магнитосопротивления по току из вольт-амперной характеристики, который объясняется в модели изменения доменной структуры во внешнем электрическом поле.

21. Получено выражение для температуры Нееля и низкотемпературной теплоемкости двухслойного квазидвумерного антиферромагнетика [В.В.Вальков и др. ТМФ, 168, 417 (2011)]. Показано, что константы межплоскостного обменного взаимодействия входят в это выражение в виде их среднего геометрического. Обнаружено, что наличие магнитного поля приводит к появлению отрицательного линейного по температуре вклада в низкотемпературную теплоемкость двухслойного антиферромагнетика.

22. В первом боровском приближении рассчитана зависимость дважды дифференциального сечения неупругого магнитного рассеяния нейтронов на соединении LaCoO₃, помещенного в магнитное поле, в парамагнитной фазе от энергии рассеянных нейтронов [А.Д.Федосеев. ЖЭТФ, 146, 651 (2014)]. Проведена оценка амплитуды пика в этой зависимости, соответствующего переходу между низкоспиновым и среднеспиновым состоянием.

23. Исследована динамическая восприимчивость и одномерная плотность состояний в изначально синусоидальной сверхрешетке с одновременным присутствием 2D фазовых неоднородностей, моделирующих коррелированные шероховатости интерфейсов сверхрешетки, и 3D амплитудных неоднородностей материала слоев сверхрешекти. Показано, что обнаруженный ранее эффект асимметрии величин пиков динамической восприимчивости на границе зоны Бриллюэна сверхрешетки под действием 2D неоднородностей проявляется также и в форме функции плотности состояний.

    Показано также, что рост среднеквадратичных флуктуаций 3D амплитудных неоднородностей в сверхрешетке, содержащей 2D фазовые недонородности, приводит к подавлению эффекта асимметрии пиков динамической восприимчивости и к некоторому росту ширины щели в плотности состояний при уменьшении ее глубины [В.А. Игнатченко и др. ЖЭТФ, 140, 268 (2011)].

24. Изучена динамическая восприимчивость (функция Грина) и плотность состояний волн в сверхрешетке для ситуации плавного перехода между 3D и 1D неоднородностями [V.A. Ignatchenko et al. Solid State Phenomena, 168-169, 85 (2011)]. Анизотропная корреляционная функция неоднородностей имеет различные корреляционные радиусы вдоль оси z и в плоскости xy сверхрешетки.

    Анизотропия корреляций характеризуется параметром λ, который меняется от 0 (изотропные 3D неоднородности) до 1 (1D неоднородности). Пики мнимой части функции Грина на краях щели в спектре волн с увеличением λ сближаются, их ширины увеличиваются и они сливаются в один пик в точке перехода от 3D к 1D неоднородностям.

    Показано, что хотя система неоднородностей остается трехмерной вплоть до критической точки, соответствующей переходу к 1D симметрии, все спектральные свойства меняются плавно с ростом λ, постепенно приближаясь к значениям, соответствующим 1D неоднородностям.

25. Исследован спектр спиновых волн в одномерных магнонных кристаллах и синусоидальных сверхрешетках при периодической модуляции всех основных магнитных параметров материала: обмена, магнитной анизотропии и намагниченности.

    Вычислены зависимости ширины запрещенной зоны в спектре как от разности магнитных параметров в соседних слоях, так и от соотношения толщин слоев [V.A. Ignatchenko et al. Solid State Phenomena, 190, 71 (2012)].

26. Исследованы динамические восприимчивости (функции Грина) системы двух связанных волновых полей различной физической природы в среде как с нулевым средним значением параметра связи [В.А. Игнатченко и др. ЖЭТФ 143, 238 (2013)], так и с произвольным соотношением между его средним значением и среднеквадратичной флуктуацией [В.А. Игнатченко и др. ЖЭТФ 144, 972 (2013)].

    Получены выражения диагональных и недиагональных элементов матричной функции Грина. Численно исследованы изменения формы диагональных элементов с приближенным учетом многократного рассеивания волн на 1D неоднородностях с ростом среднеквадратичной флуктуации и уменьшением среднего значения параметра связи при условии сохранения суммы квадратов этих величин: уширение и последующее слияние двух пиков на мнимых частях диагональных элементов матричной функции Грина в один широкий пик; возникновение и формирование тонкой структуры в форме узкого резонанса на вершине функций Грина одного волнового поля и узкого антирезонанса на вершине функции Грина другого поля; рост ширины пиков тонкой структуры и последующее исчезновение их с ростом корреляционного волнового числа неоднородностей параметра связи, уменьшение амплитуд недиагональных элементов до нуля при стремлении к нулю среднего значения параметра связи.

27. Получено аналитическое решение уравнения для спектрального представления функции Грина в синусоидальной сверхрешетке в виде комбинации восходящих и нисходящих быстро сходящихся цепных дробей. Получены и исследованы приближенные аналитические выражения для функций Грина в r-пространстве в области частот, включающей первую и вторую зоны Бриллюэна и запрещенную зону между ними [V.A. Ignatchenko et al. Solid State Phenomena, 233-234, 47 (2015)].