Advanced Results

• With regard to the scattering on spin fluctuations, we developed the theory of a superconducting phase with the d-type symmetry of the order parameter, experimentally observed in cuprate oxides. We showed that in the description of the spin fluctuation scattering processes, an important role is played by the anomalous components of the force operator, which were introduced by us for the first time. This modifies the Gor’kov equations and significantly affects the calculated anomalous means in the Hubbard fermion subsystem [V. V. Val'kov et al., JETP 134, 1167 (2008)].

• For the first time, we demonstrated that the interstitial Coulomb interaction in Mott--Hubbard dielectrics leads to splitting of the lower Hubbard band into two subbands [V.V. Val’kov et al., Eur. Phys. J. B 69, 219 (2009); V.V. Val’kov et al., JETP 139, 126 (2011)] as soon as the characteristic value of this interaction becomes comparable with of exceeds the kinetic energy of Hubbard fermions. It is important that the spectral intensity of the lower band (fluctuation state band) depends on the root-mean-square fluctuation of the occupation numbers and grows with the doping level.

• Within the effective model for the 2D Kondo lattice, we developed the theory of the superconducting phase of an ensemble of spin polarons. Taking into account the effective interactions between such quasi-particles, we built the phase diagram determining the region of implementation of the superconducting phase.

• For the real structure of the CuO₂ plane of cuprate superconductors, we obtained the energy structure of nonlocal spin polarons and considered the Cooper instability in an ensemble of such Fermi quasiparticles. A nonlocal spin polaron forms due to the exchange interaction of the spin angular momentum of an oxygen hole and the spin moments of two nearest copper ions. The scattering amplitude of nonlocal spin polarons in a Cooper channel calculated using a diagram technique revealed the strong correlation between the spin and charge degrees of freedom [V. Valkov et al., JETP Lett. 92, 683 (2010)].

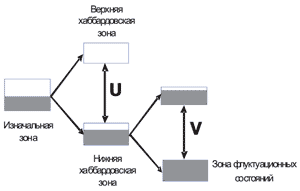
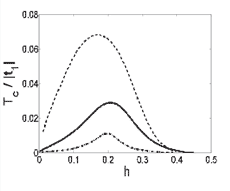
  Fig. 1. Schematic of the splitting of the energy bands in a system with the strong electron correlations under the action of the one-site and interstitial Coulomb interactions.	Fig. 2. Concentration dependences of TC for finite (solid curve) and zero (dashed curve) values of the magnetic correlators.

• Using the periodic Anderson model in the limit of strong electron correlations, we developed the theory of the superconducting state with the s-type symmetry of the order parameter [V.V. Val’kov et al., JETP Lett. 84, 251 (2006); V.V.Val’kov et al., JETP 134, 791 (2008)]. The phase transition to such a state has been experimentally observed in the recently discovered heavy-fermion skutterudite LaFe₄P_12. We obtained the exact representations of the Green’s function of the superconducting phase via normal and anomalous components of mass and force operators. We demonstrated that a key role in the description of the superconducting phase is played by anomalous components of the strength operator, which reflects spin fluctuations in a localized subsystem. In the one-loop approximation, these components were calculated by solving an infinite system of integral self-consistency equations for the superconducting phase. According to the numerical calculations, inclusion of scattering on spin fluctuations leads to renormalization of the critical temperature to the one observed in the experiment.

• Under the condition of sublattices canted in a magnetic field, we developed the theory of antiferromagnetic rare-earth heavy-fermion intermetallides [V.V. Val’kov et al., Physica B: Condensed Matter 378-380, 692 (2006)]. Taking into account rearrangement of the magnetic subsystem, we established the low-temperature features of electron specific heat of heavy-fermion antiferromagnets with the metal-type ground state [V.V. Val’kov et al., Theor. Math. Phys. 162, 125 (2010); V.V. Val’kov et al., JETP 137, 341 (2010)]. The calculated temperature dependences of magnetization, specific heat, and the Sommerfeld constant in the vicinity of the point of transition to the antiferromagnetic phase are in good agreement with the experimental data for heavy-fermion antiferromagnets PuGa₃, Ce₂Au₂Cd, YbNiSi₃, and PuPd₅Al₂.

• In cooperation with researches of the Laboratory of Strong Magnetic Fields, we proposed a model of Schottky centers in the CuO_x chains of the YBa₂Cu₃O_6+x compound [K.A. Shaikhutdinov et al., JRTP Lett. 92, 369 (2010)]. The model allowed us to explain experimental features of low-temperature specific heat in a magnetic field. We suggested that an increase in the oxygen concentration leads to the formation of single Cu₂₊ ions and five-ion Cu-O-Cu-O-Cu complexes, whose energy structure is built with regard to the crystal field of the cubic symmetry with the orthorhombic addition, spin-orbit interaction, and splitting in a magnetic field.

• We developed a theory for the rare-earth intermetallic compound CeRhIn₅ [V.V. Val’kov et al., JETP Lett. 95, 350 (2012)], which describes the superconducting state in the vicinity of the quantum critical point, where the long-range antiferromagnetic order is induced. We showed that Cooper pairing and antiferromagnetic ordering are caused by the effective exchange interaction, which emerges due to hybridization between indium p-electrons and high-energy states of the cerium ion subsystem. We established the pressure range where the phase of microscopically homogeneous coexistence of superconductivity and antiferromagnetism is implemented.

  

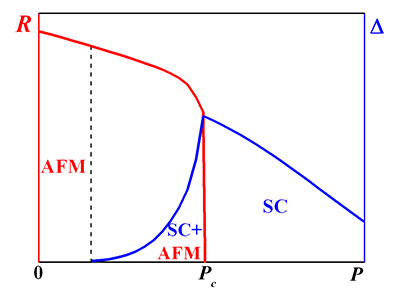
  Fig. 3. Pressure dependences of antiferromagnetic R and superconducting Δ order parameters for the rare-earth intermetallic compounds with heavy fermions. The regions of antiferromagnetic phase (AFM), superconducting phase (SC), and the superconductivity and antiferromagnetism coexistence phase (SC + AFM) are shown.

• By an example of CeRhIn₅, we demonstrated that at the quantum phase transition with the long-range antiferromagnetic order break, the Fermi surface is significantly extended and the effective electron mass is strongly renormalized. This is due to to reconstruction of the heavy-fermion band when passing through the quantum critical point.
• Using the spin-fermion model, we showed that the spin-polaron concept allows reproducing subtle features of the Fermi surface evolution in the high-temperature superconductor La_2-xSr_xCuO₄ [DM Dzebisashvili et al., JETP Lett. 98, 596 (2013)]. The spin-correlated hopping of carriers and variation in the reverse magnetic correlation length with doping are important.

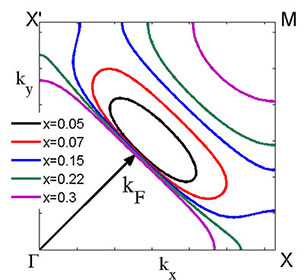
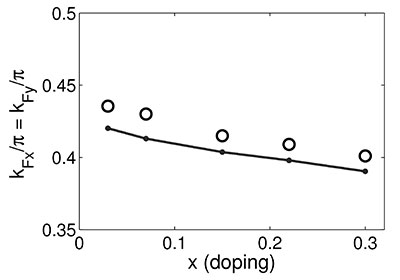
  Fig. 4. Fermi surfaces in the Brillouin zone first quadrant for five doping concentrations x.	Fig. 5. Dependence of Fermi momentum kF on doping concetration x. Solid line shows kF values calculated using the spin-polaron approach and open circles show experimental kF values reported in [T. Yoshida et al., J. Phys .: Condens. Matter 19, 125209 (2007)].

• Based on the effective Hamiltonian of the 2D Emery model in the spin-polaron approach, we studied the effect of spin and multicenter spin-charge correlators on the spectral properties of cuprate high-temperature superconductors [V. Valkov et al., JETP 145, 1087 (2014)]. The results of self-consistent calculations showed that the account for the concentration-dependent multicenter spin-charge correlators included in the dispersion equation provides a decrease in system energy and significantly affects the Fermi surface evolution at hole doping.

  

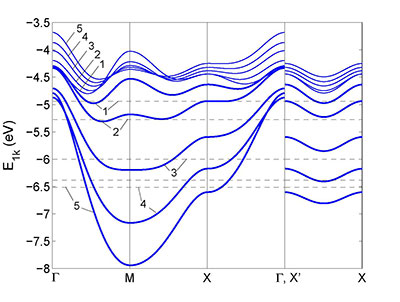
  Fig. 6. Dispersion curves of the lower spin polaron band. Bold curves show the calculation with regard to all the correlation functions for five doping concentrations: (1) x = 0.03, (2) 0.07, (3) 0.15, (4) 0.22, and (5) 0.3. The dashed line indicates the chemical potential position. Thin lines are the dispersion curves calculated for the same x values, but with regard to the spin correlators only.

• We demonstrated that the strong coupling between spin moments of copper ions and oxygen holes, which arises upon hybridization mixing of two hole subsystems in the Emery model, not only affects the formation of spin polaron quasiparticles, but also ensures effective attraction between them via the exchange interaction [V.V. Val'kov et al., Phys. Lett. A 379, 421 (2015); V.V. Val'kov et al., J. Low-Temperature Phys. 181, 134 (2015)]. This results in Cooper instability with d-wave pairing in a 2D ensemble of spin polaron quasiparticles. The T-x phase diagram obtained using this approach agrees well with the available experimental data.

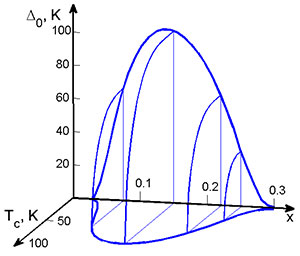
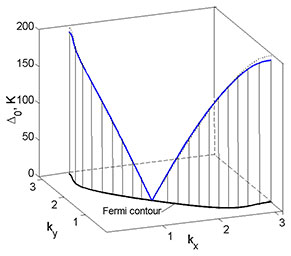
  Fig. 7. Variation in the amplitude of the d-wave superconducting order parameter Δ0 and superconducting transition temperature Tc upon doping.	Fig. 8. Superconducting gap vs quasimomentum on the Fermi contour. The Fermi contour is indicated by the solid line in the horizontal plane. The calculation was made for x = 0.125.

• Using the Shubin–Vonsovsky model in the weak-coupling regime based on the Kohn-Luttinger mechanism, we determined the regions of existence of the superconducting phases with the dxy, p, s, and dx2-y2 symmetry types of the order parameter. We showed that the effective interaction in the Cooper channel significantly depends on both one-site and interstitial Coulomb correlations. It was confirmed by the qualitative change and complication of the phase diagram of the superconducting state. The mechanism of induction of the superconducting phase is determined taking into account polarization contributions in the second-order perturbation theory in the Coulomb interaction. The obtained angular dependences of the superconducting gap in different channels were compared with angle-resolved photoemission spectroscopy (ARPES) data. The influence of long-range hoppings on the phase diagram and critical superconducting transition temperature in different channels was analyzed. The conditions for the appearance of the Kohn–Luttinger superconductivity with the symmetry and high critical temperature Tc ~ 100 K near the half-filling were established.

  

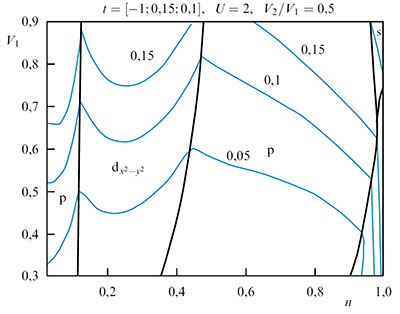
  Fig. 9. Phase diagram of the Kohn-Luttinger superconducting state in the Shubin-Vonsovsky model on the square lattice.

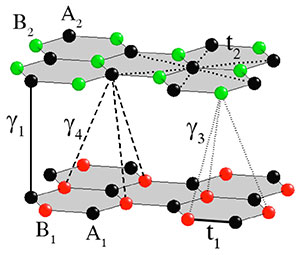
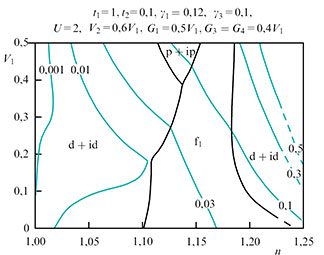
• We explored the effect of Coulomb interaction in a Dirac fermion ensemble on superconducting pairing in monolayer and bilayer doped graphene using the Kohn-Luttinger mechanism with disregard of the van der Waals potential of the substrate and impurities. The electronic structure of graphene is described using the Shubin−Vonsovsky model, taking into account the intratomic, interatomic, and interlayer (in the case of bilayer graphene) Coulomb interactions between electrons. We showed that the allowance for Kohn−Luttinger renormalizations, as well as the intersite Coulomb interaction, noticeably affects the competition between the superconducting phases with the f-wave, p+ip-wave, and d+id-wave order parameter symmetries. We demonstrated that the superconducting transition temperature for an idealized graphene bilayer with the significant interlayer Coulomb interaction between electrons is noticeably higher than in the monolayer case.

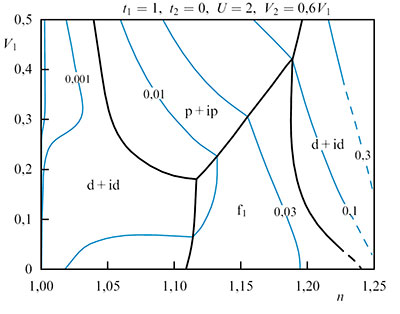
Fig. 10. Phase diagram of the Kohn−Luttinger superconducting state in the idealized graphene monolayer.

Fig. 11. Crystal lattice of the AB-stacking graphene bilayer.	Fig. 12. Phase diagram of the Kohn−Luttinger superconducting state in the idealized graphene bilayer.

• We developed the microscopic theory of the transport properties of magnetic multilevel atomic-scale structures, which takes into account multiple inelastic scattering.
• We disclosed the effect of negative differential conductance, spin filtering, and colossal magnetoresistance in magnetic atomic-scale structures.

  

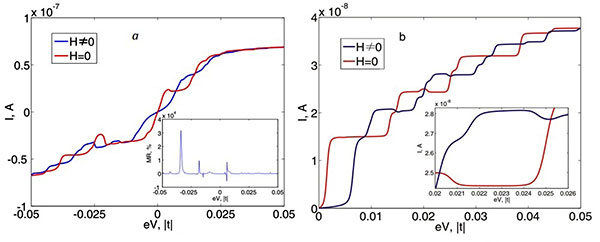
  Fig. 13. Influence of magnetic field H on the I−V characteristics of an anisotropic magnetic atom. Inset to (a): colossal magnetoresistance. Inset to (b): negative differential conductance.

• We built the quantum theory of four-sublatice anisotropic Heisenberg magnets and calculated the low-temperature magnetic properties of the single-chain magnet catena-[Fe^II(ClO₄)₂{Fe^III(bpca)₂}](ClO₄) (hereinafter, SCM-catena) with four sublattices and twisting mutually orthogonal easy planes of iron ions. We showed that the excitation spectrum of the compound is similar to that of a two-sublattice magnet with the effective easy axis [V.V. Val’kov et al., Bull. Russ. Acad. Sci. Phys. (2015)]. Using the data on the spectral and magnetic properties of the compound, we strictly established that the generalized Ising model is an effective model of the SCM-catena at low temperatures. This allowed us to describe modification of magnetic susceptibility of the compound under optical irradiation [V.V. Val’kov et.al., JETP Lett. (2014)]. We showed that the presence of easy planes of iron ions in the SCM-catena leads to significant development of quantum fluctuations, which should be taken into account in phenomenological description of the magnetic properties of the SCM-catena in the framework of the Ising model. Modification of the magnetic structure of the compound under optical irradiation was elucidated [V.V. Val’kov et al, JETP (2015)].

  

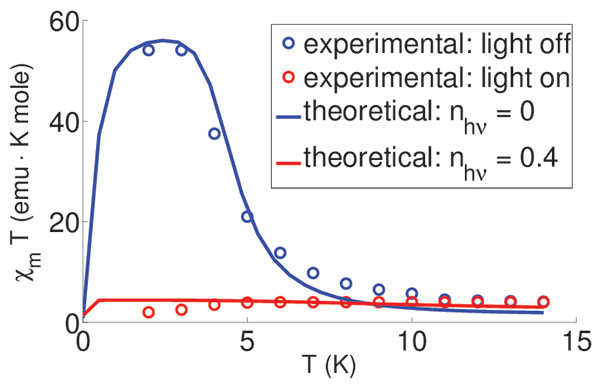
  Fig. 14. Modification of the temperature dependence of magnetic susceptibility of catena -[{FeIIClO4)2FeIII(bpca)2]ClO4 without irradiation (theory - blue solid line 1 and experiment - blue circles) and under irradiation (theory – red solid line and experiment - red circles).

• We obtained the expression for Neel temperature of a quasi-2D bilayer antiferromagnet [V.V. Val’kov et al., Theor. Math. Phys. 168, 417 (2011)] and showed that it is expressed via the geometric mean of the interplane exchange parameters.
• We calculated the partial differential cross-section of inelastic magnetic neutron scattering from the LaCoO₃ compound in the paramagnetic phase in a magnetic field [A.D. Fedoseev, JETP 119, 573 (2014)]. The amplitude of the peak in the dependence of the scattering cross-section on the energy of scattered neutrons, which corresponds to the transition from the low-spin to intermediate-spin state, was estimated.
• We investigated the dynamic susceptibility (Green's function) and density of states in an initially sinusoidal superlattice, which simultaneously contains 2D phase inhomogeneities simulating correlated roughness of the superlattice interfaces and 3D amplitude inhomogeneities of the superlattice layer material. We established that the previously discovered effect of asymmetry in the peak heights of dynamic susceptibility at the Brillouin zone boundary of the superlattice takes place also in the form of the density of states. We demonstrated that enhancement of rms fluctuations of 3D-amplitude inhomogeneities in a superlattice containing 2D-phase inhomogeneities suppresses the effect of dynamic susceptibility asymmetry and leads to slight broadening of the gap in the density of states and to a decrease in its depth [V.A. Ignatchenko et al., JETP 113, 232 (2011)].
• We examined the dynamic susceptibility and density of states of waves in a superlattice at the smooth transition between 3D and 1D inhomogeneities [V.A. Ignatchenko et al., Solid State Phenom. 168-169, 85 (2011)]. The anisotropic correlation function has different correlation radii along the superlattice z axis and in the xy plane. The anisotropy of the correlations was characterized by parameter λ, which varies from 0 (isotropic 3D inhomogeneities) to 1 (1D inhomogeneities). The peaks of the imaginary part of the Green's function at the edges of the gap in the spectrum of waves with increasing λ approach one another, broaden, and merge in a single peak at a point of the transition from 1D to 3D inhomogeneities. We showed that, although the system of inhomogeneities remains three-dimensional until the critical point corresponding to the transition to the 1D symmetry, the spectral properties change gradually with increasing λ, approaching the values corresponding to 1D inhomogeneities.
• We studied the spin-wave spectrum in 1D magnon crystals and sinusoidal superlattices for periodic modulation of all basic parameters of the material, including exchange, magnetic anisotropy, and magnetization. The dependences of band gaps in the spectrum on the difference between magnetic parameters in adjacent layers and the ratio between layer thicknesses were calculated [V.A. Ignatchenko et al., Solid State Phenom. 190, 71 (2012)].
• We examined dynamic susceptibilities (Green’s functions) of the system of two coupled wave fields of different physical natures in a medium as a zero-mean value of the coupling parameter [V.A. Ignatchenko et al., JETP 116, 206 (2013)] and an arbitrary relation between its mean value and rms fluctuation [V.A. Ignatchenko et al., JETP 117, 846 (2013)]. We obtained expressions for diagonal and off-diagonal elements of the matrix Green's function. Variation in the form of diagonal elements were numerically studied with regard to multiple scattering of waves on 1D inhomogeneities with an increase in the rms fluctuation and with a decrease in the average value of coupling parameter under the condition of the conserved sum of the squares of these quantities. We found out the following: (i) two peaks in the frequency dependences of imaginary parts of diagonal elements of the matrix Green's function broaden and then merged into one broad peak; (ii) a fine structure appears in the form of narrow resonance at the vertex of the Green’s function of one wave field and narrow antiresonance at the vertex of the Green’s function of the other field; (iii) the fine structure peaks broaden and then vanish with an increase in the correlation wavenumber of coupling parameter inhomogeneities; (iv) the amplitudes of off-diagonal elements vanish when the average value of the coupling parameter vanishes.
• We found the analytical expression for spectral representation of the Green's function in the form of ascending and ordinary quickly converging continued fractions. The approximate analytical expression for the Green's function in the r-space in the frequency range from zero to the second gap was obtained [V.A. Ignatchenko et al., Solid State Phenom. 233, 47 (2015)].